The Simplified - Sequential Minimal Optimization (SMO) Algorithm - Support Vector Machines

Stanford CS229 - Andrew Ng

Introduction

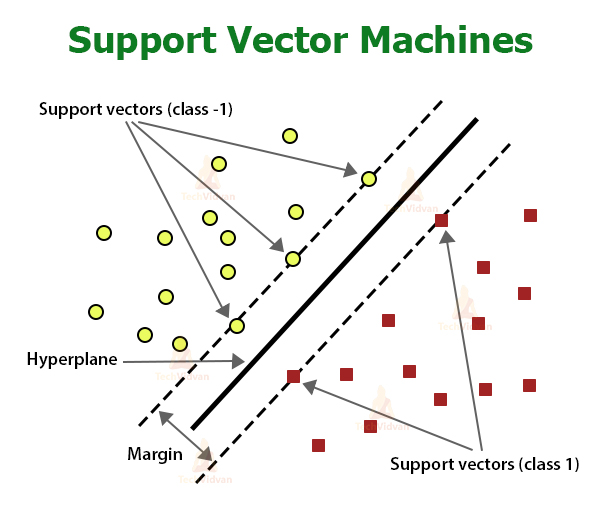
This notebook implements the Simplified - SMO algorithm of Support Vector Machines. It performs binary classification on a generated dataset consisting of two gaussian distributed clusters of points in a 2-dimensional space. The support vectors are visually shown forming a boundary between the two clusters of points. The prediction accuracy for a learning dataset of 100 points is 98-100%.

Resources:

The Simplified - SMO algorithm differs from the original SMO algorithm by John Platt only in the choice of the data point ‘j’, given a chosen data point ‘i’ while performing gradient descent on a pair of points at a time.

Towards the end, I have included a sidebar on the Primal to Dual Problem.

Taxonomy

SVM is not probabilistic. SVM takes a geometric approach to classification. It is a discriminative classifier. It is a binary classification algorithm. The classifier finds a linear hyperplane separating the two classes of data points. It is parametric, with weights and a bias for the features, and lagrange multipliers for the constraints.

Multi-class SVM can be developed using a one-vs-one or a one-vs-all approach.

In summary, a SVM classifier is:

Non-Probabilistic, Geometric
Discriminative
Binary
Linear
Parametric

Imports

import numpy as np #arrays for data points
from numpy.random import normal, randint #gaussian distributed data points
from numpy import dot #vector dot product for the linear kernel
import pandas as pd #create dataframe from data points, for plotting using sns
import matplotlib.pyplot as plt #plotting
import seaborn as sns #plotting
%matplotlib inline

X_m, Y

Data Configuration

M = 100 #number of data points
n_features = 2 #number of dimensions
cols = ['X1', 'X2', 'Y'] #column names of the dataframe
K = 2 #number of classes
loc_scale = [(5, 1), (8, 1)] #mean and std of data points belonging to each class

Generate Data

Gaussian clusters in 2D numpy arrays

def generate_X_m_and_Y(M, K, n_features, loc_scale):
    #X_m, Y
    X_m = np.empty((K, (int)(M/2), n_features), dtype=float) #initialize data points
    Y = np.empty((K, (int)(M/2)), dtype=int) #initialize the class labels
    for k in range(K): #for each class, generate data points #create data points for each class
        #create data points for class k using gaussian (normal) distribution
        X_m[k] = normal(loc=loc_scale[k][0], scale=loc_scale[k][1], size=((int)(M/2), n_features))
        #create labels (-1, +1) for class k (0, 1).
        #trick: for k=0, label is -1+2*0=-1; for k=1, label is -1+2*1=1
        Y[k] = np.full(((int)(M/2)), -1 + 2*k, dtype=int)
    X_m = X_m.reshape(M, K) #collapse the class axis
    Y = Y.reshape(M) #collapse the class axis
    X_m.shape, Y.shape #print shapes
    
    return X_m, Y

X_m, Y = generate_X_m_and_Y(M, K, n_features, loc_scale)

X_m, Y in DataFrame

def create_df_from_array(X_m, Y, n_features, cols):
    #create series from each column of X_m, and a series from Y
    l_series = [] #list of series, one for each column
    for feat in range(n_features): #create series from each column of X_m
        l_series.append(pd.Series(X_m[:, feat])) #create series from a column of X_m
    l_series.append(pd.Series(Y[:])) #create series from Y

    frame = {col : series for col, series in zip(cols, l_series)} #map of column names to series
    df = pd.DataFrame(frame) #create dataframe from map

    return df

df = create_df_from_array(X_m, Y, n_features, cols)
df.sample(n = 10)

	X1	X2	Y
40	5.211933	3.162270	-1
96	7.682917	9.953946	1
22	2.870566	5.851050	-1
43	3.325478	3.798079	-1
59	7.752266	8.119911	1
52	7.489131	8.838146	1
2	4.896474	4.321929	-1
57	10.056611	7.791627	1
84	8.746390	7.573401	1
32	5.165944	5.219445	-1

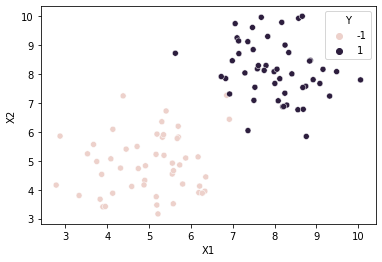
#scatter plot of data points
#class column Y is passed in as hue
sns.scatterplot(x=cols[0], y=cols[1], hue=cols[2], data=df)

<AxesSubplot:xlabel='X1', ylabel='X2'>

png

Model

Model Configuration

#cost to pay if functional margin is < 1
C = 0.6 #regularization parameter

#tolerance for meeting the KKT conditions that are used to check for convergence
tol = 0.001 #tolerance

#number of iterations to perform after the alphas have converged
max_passes = 5

Model Prediction Data Structures

Note that alphas and bias are created here for testing the functions that follow. They will be created fresh inside the SMO algorithm.

#estimated lagrangian Multipliers
#most of the alphas will be close to zero, except for alphas of data points that are support vectors
alphas = np.zeros((M), dtype=float) #one multiplier for each data point

#bias of the dual problem
#in the primal problem, we have both w (weights) and b (bias).
#in the dual problem, w is replaced with alpha, but b remains.
bias = 0.0

Linear Kernel

'''linear kernel : compute the dot product of the 2 vectors
    
    returns:
        (float) the dot product of the 2 vectors
        
    parameters:
        X1: the first vector
        X2: the second vector
'''
def k_lin(X1, X2):
    return dot(X1, X2)

Predict (eq 2)

$f\left ( x \right )= \sum_{i=1}^{m}\alpha _{i}y^{\left ( i \right )}\left \langle x^{\left ( i \right )}, x \right \rangle + b$

'''predict the label given the input, training data, and learnt parameters alphas and bias.
    this is equivalent to WX + b, but using alphas instead of W.
'''
def fx(X, X_m, Y, alphas, bias, knl = k_lin):
    pred = 0.0
    for i, Xi in enumerate(X_m):
        pred += alphas[i] * Y[i] * knl(Xi, X)
    
    return pred + bias

fx(X_m[0], X_m, Y, alphas, bias)

0.0

Error for a data point (eq 13)

$E_{k}=f\left ( x^{\left ( k \right )} \right )-y^{\left ( k \right )}$

'''error between the SVM output and the true label
'''
def Err(X, y, X_m, Y, alphas, bias, knl = k_lin):
    #predict the label
    y_pred = fx(X, X_m, Y, alphas, bias, knl)
    
    return y_pred - (float)(y)

Err(X_m[0], Y[0], X_m, Y, alphas, bias)

1.0

KKT Dual Complementarity Conditions (eq 6-8)

$\alpha _{i}= 0\Rightarrow y^{\left ( i \right )}\left ( w^{T}x^{\left ( i \right )}+b \right )\geq 1$

$\alpha _{i}=C\Rightarrow y\left ( i \right )\left ( w^{T}x^{\left ( i \right )} +b\right )\leq 1$

$0< \alpha _{i}< C\Rightarrow y\left ( i \right )\left ( w^{T}x^{\left ( i \right )} +b\right )= 1$

The above equations translate into the following pseudo-code:

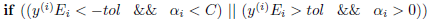
'''Karush-Kuhn-Tucker conditions
'''
def kkt(y, err, alpha):
    if ((y * err < -tol) and (alpha < C)) or \
    ((y * err > tol) and (alpha > 0)):
        return True
    
    return False

err = Err(X_m[0], Y[0], X_m, Y, alphas, bias)
kkt(Y[0], err, alphas[0])

True

L and H - boundary constraints on alphas (eq 10-11)

$y^{\left ( i \right )}\neq y^{j} \Rightarrow L = max(0, \alpha _{j}-\alpha _{i}), H = min(C, C+\alpha _{j}-\alpha _{i}))$

$y^{\left ( i \right )}= y^{j} \Rightarrow L = max(0, \alpha _{i}+\alpha _{j}-C), H = min(C, \alpha _{i}+\alpha _{j}))$

def LH(yi, yj, ai, aj):
    if yi != yj:
        L, H = max(0, aj-ai), min(C, C+aj-ai)
    else:
        L, H = max(0, ai+aj-C), min(C, ai+aj)
        
    #if(L > H):
        #print('L IS GREATER THAN H: L=', L, ' H=', H, ' yi=', yi, ' yj=', yj, ' ai=', ai, ' aj=', aj)
        
    return L, H

LH(Y[0], Y[1], alphas[0], alphas[1])

(0, 0.0)

n - denominator when calculating optimal alpha_j (eq 14)

$\eta =2\left ( x^{\left ( i \right )},x^{\left ( j \right )} \right )-\left ( x^{\left ( i \right )},x^{\left ( i \right )} \right )-\left ( x^{\left ( j \right )},x^{\left ( j \right )} \right )$

'''denominator when calculating optimal alpha_j
'''
def n_den(Xi, Xj, knl = k_lin):
    return 2 * knl(Xi, Xj) - knl(Xi, Xi) - knl(Xj, Xj) #TODO line 63 return (-1) *

n_den(X_m[0], X_m[1])

-1.6061731002951376

alpha_j (eq 12)

$\alpha _{j}:= \alpha _{j}-\frac{y^{\left ( j \right )}\left ( E_{i}-E_{j} \right )}{\eta }$

def alpha_j(aj, yj, err_i, err_j, n):
    return aj - ((yj * (err_i - err_j)) / n) #TODO line 65 aj + 

i, j = 0, M-1
Xi, Xj, Yi, Yj = X_m[i], X_m[j], Y[i], Y[j]
err_i = Err(Xi, Yi, X_m, Y, alphas, bias)
err_j = Err(Xj, Yj, X_m, Y, alphas, bias)
n = n_den(Xi, Xj)
aj = alpha_j(alphas[j], Yj, err_i, err_j, n)
print('Xi=', Xi, 'Yi=', Yi)
print('Xj=', Xj, 'Yj=', Yj)
print('err_i=', err_i, 'err_j=', err_j, 'n=', n, 'aj=', aj)

Xi= [2.7774898  4.15832218] Yi= -1
Xj= [6.98985299 8.45370087] Yj= 1
err_i= 1.0 err_j= -1.0 n= -36.19428180189391 aj= 0.05525734730548922

clipped / constrained alpha_j (eq 15)

$\alpha _{j}:=\left\{\begin{matrix} H & if\: \alpha _{j} > H \\ \alpha _{j} & if\: L \leq \alpha _{j} \leq H\\ L & if\; \alpha _{j} < L \end{matrix}\right.$

def clip_alpha_j(aj, L, H):
    if aj > H:
        return H
    elif (L <= aj and aj <= H):
        return aj
    else:
        return L

i, j = 0, M-1
Xi, Xj, Yi, Yj = X_m[i], X_m[j], Y[i], Y[j]
err_i = Err(Xi, Yi, X_m, Y, alphas, bias)
err_j = Err(Xj, Yj, X_m, Y, alphas, bias)
n = n_den(Xi, Xj)
aj = alpha_j(alphas[j], Yj, err_i, err_j, n)
print('aj_old=', alphas[j], 'aj_new=', aj)
L, H = LH(Y[i], Y[j], alphas[i], aj)
aj = clip_alpha_j(aj, L, H)
print('L=', L, 'H=', H, 'aj_clipped=', aj)

aj_old= 0.0 aj_new= 0.05525734730548922
L= 0.05525734730548922 H= 0.6 aj_clipped= 0.05525734730548922

alpha_i (eq 16)

$\alpha _{i}:=\alpha _{i}+y^{\left ( i \right )}y^{\left ( j \right )}\left ( \alpha _{j}^{\left ( old \right )} -\alpha _{j}\right )$

def alpha_i(ai, aj_old, aj, yi, yj):
    return ai + (yi * yj * (aj_old - aj))

i, j = 0, M-1
Xi, Xj, Yi, Yj = X_m[i], X_m[j], Y[i], Y[j]
err_i = Err(Xi, Yi, X_m, Y, alphas, bias)
err_j = Err(Xj, Yj, X_m, Y, alphas, bias)
n = n_den(Xi, Xj)
aj = alpha_j(alphas[j], Yj, err_i, err_j, n)
print('aj_old=', alphas[j], 'aj_new=', aj)
L, H = LH(Y[i], Y[j], alphas[i], aj)
aj = clip_alpha_j(aj, L, H)
print('L=', L, 'H=', H, 'aj_clipped=', aj)
ai = alpha_i(alphas[i], alphas[j], aj, Yi, Yj)
print('ai_old=', alphas[i], 'ai_new=', ai)

aj_old= 0.0 aj_new= 0.05525734730548922
L= 0.05525734730548922 H= 0.6 aj_clipped= 0.05525734730548922
ai_old= 0.0 ai_new= 0.05525734730548922

b1, b2, b (eq 17-19)

$b_{1}=b-E_{i}-y^{\left ( i \right )}\left (\alpha _{i}-\alpha _{i}^{\left ( old \right )} \right )\left \langle x^{\left ( i \right )},x^{\left ( i \right )} \right \rangle-y^{\left ( j \right )}\left ( \alpha _{j}-\alpha _{j}^{\left ( old \right )} \right )\left \langle x^{\left ( i \right )},x^{\left ( j \right )} \right \rangle$

def b1(Xi, Xj, Yi, Yj, ai_old, ai, aj_old, aj, b, err_i, knl = k_lin):
    return b - err_i - Yi * (ai - ai_old) * knl(Xi, Xi) - Yj * (aj - aj_old) * knl(Xi, Xj)

$b_{2}=b-E_{j}-y^{\left ( i \right )}\left (\alpha _{i}-\alpha _{i}^{\left ( old \right )} \right )\left \langle x^{\left ( i \right )},x^{\left ( j \right )} \right \rangle-y^{\left ( j \right )}\left ( \alpha _{j}-\alpha _{j}^{\left ( old \right )} \right )\left \langle x^{\left ( j \right )},x^{\left ( j \right )} \right \rangle$

def b2(Xi, Xj, Yi, Yj, ai_old, ai, aj_old, aj, b, err_j, knl = k_lin):
    return b - err_j - Yi * (ai - ai_old) * knl(Xi, Xj) - Yj * (aj - aj_old) * knl(Xj, Xj)

$b:=\left\{\begin{matrix} b_{1} & if\; 0<\alpha _{i}<C \\ b_{2} & if\; 0< \alpha _{j}<C\\ \left (b_{1}+b_{2} \right )/2 & otherwise \end{matrix}\right.$

def b(b1, b2, ai, aj):
    if (ai > 0 and ai < C):
        return b1
    elif (aj > 0 and aj < C):
        return b2
    else:
        return (b1 + b2)/2

i, j = 0, M-1
Xi, Xj, Yi, Yj = X_m[i], X_m[j], Y[i], Y[j]
err_i = Err(Xi, Yi, X_m, Y, alphas, bias)
err_j = Err(Xj, Yj, X_m, Y, alphas, bias)
n = n_den(Xi, Xj)
ai_old = alphas[i]
aj_old = alphas[j]
aj = alpha_j(aj_old, Yj, err_i, err_j, n)
print('aj_old=', aj_old, 'aj_new=', aj)
L, H = LH(Y[i], Y[j], ai_old, aj)
aj = clip_alpha_j(aj, L, H)
print('L=', L, 'H=', H, 'aj_clipped=', aj)
ai = alpha_i(ai_old, aj_old, aj, Yi, Yj)
print('ai_old=', ai_old, 'ai_new=', ai)

b1_val = b1(Xi, Xj, Yi, Yj, ai_old, ai, aj_old, aj, bias, err_i)
print('b1=', b1_val)
b2_val = b2(Xi, Xj, Yi, Yj, ai_old, ai, aj_old, aj, bias, err_j)
print('b2=', b2_val)
b_val = b(b1_val, b2_val, ai, aj)
print('b=', b_val)

aj_old= 0.0 aj_new= 0.05525734730548922
L= 0.05525734730548922 H= 0.6 aj_clipped= 0.05525734730548922
ai_old= 0.0 ai_new= 0.05525734730548922
b1= -2.6334825719646275
b2= -2.6334825719646275
b= -2.6334825719646275

select random j

#select a j not equal to i
def sel_rand_j(i):
    j = randint(M) #select a random number j in the range 0..M-1
    while (j==i): #while we got i as the random number, in which case j == i, we keep trying a different random number
        j = randint(M) #try a different random number
    return j #now we have a random number in the range 0..M that is not equal to i

Simplified SMO

pseudo-code

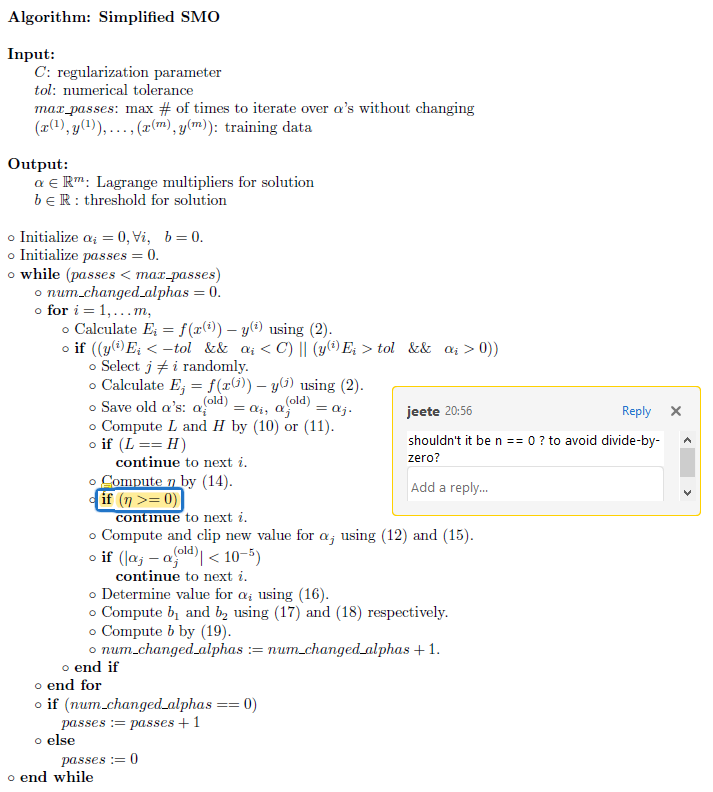
python code

def simplified_smo(C, tol, max_passes, X_m, Y, knl = k_lin):
    
    #1 Initialize alphas, and beta
    
    #estimated lagrangian Multipliers
    #most of the alphas will be close to zero, except for alphas of data points that are support vectors
    a_m = np.zeros((M), dtype=float) #one multiplier for each data point

    #bias of the dual problem
    #in the primal problem, we have both w (weights) and b (bias).
    #in the dual problem, w is replaced with alpha, but b remains.
    b_val = 0.0
    
    #2 count number of passes after the alphas have converged
    passes = 0
    
    #3 while alphas are converging, and a little beyond (max_passes beyond convergence)
    while (passes < max_passes):
        #3.1 number of alphas that changed.
        #    if they are greater than zero, we reset passes to 0. (alphas have not converged yet)
        #    if they are equal to zero, we increment passes up to max_passes, allowing alphas to converge further if they can.
        num_changed_alphas = 0
        
        #3.2 loop over the dataset, trying to converge 2 alphas
        for i in range(M):
            
            #3.2.1 calculate error between predicted label and actual label for data point i
            err_i = Err(X_m[i], Y[i], X_m, Y, a_m, b_val, knl)
            
            #3.2.2 if the KKT conditions are met
            if (kkt(Y[i], err_i, a_m[i])):
                #3.2.2.1 select j != i randomly
                j = sel_rand_j(i)
                #3.2.2.2 calculate error between predicted label and actual label for data point j
                err_j = Err(X_m[j], Y[j], X_m, Y, a_m, b_val, knl)
                #3.2.2.3 save old alphas
                ai_old, aj_old = a_m[i], a_m[j]
                #3.2.2.4 compute L and H
                L, H = LH(Y[i], Y[j], a_m[i], a_m[j])
                #3.2.2.5 if L and H are the same, we try again with a different alpha_i
                if (L == H):
                    continue
                #3.2.2.6 compute the denominator n
                n = n_den(X_m[i], X_m[j], knl)
                #3.2.2.7 if n == 0, we treat this as a case where we cannot make progress on this pair of alphas
                if (n == 0):#TODO n==0 or > =0
                    continue
                #3.2.2.8 compute and clip the new value of alpha_j
                a_m[j] = alpha_j(a_m[j], Y[j], err_i, err_j, n)
                a_m[j] = clip_alpha_j(a_m[j], L, H)
                #3.2.2.9 if alpha_j has converged, move to a new set of alphas
                if abs(a_m[j] - aj_old) < pow(10, -5): #has alpha_j converged? #TODO abs
                    continue
                #3.2.2.10 determine value of alpha_i
                a_m[i] = alpha_i(ai_old, aj_old, a_m[j], Y[i], Y[j]) # ai = ai + yi*yj*(aj_old - aj)
                #3.2.2.11 compute b1 and b2
                b1_val = b1(X_m[i], X_m[j], Y[i], Y[j], ai_old, a_m[i], aj_old, a_m[j], b_val, err_i)
                b2_val = b2(X_m[i], X_m[j], Y[i], Y[j], ai_old, a_m[i], aj_old, a_m[j], b_val, err_j)
                #3.2.2.12 compute b
                b_val = b(b1_val, b2_val, a_m[i], a_m[j])
                #3.2.2.13 increment the number of alphas changed
                num_changed_alphas += 1
            #end if 3.2.2
        #end for 3.2
        
        #3.3 if no alphas changed, increment passes a little beyond convergence
        if (num_changed_alphas == 0):
            passes += 1
        else: #some alphas changed, so we reset passes
              # and start incrementing num_changed_alphas again when alphas begin to converge
            passes = 0
            
        print('Number of lagrange multipliers still converging:', num_changed_alphas)
            
    #end while 3
    
    #return the converged alphas (lagrange multipliers), and the threshold (beta) for the solution
    return a_m, b_val

Learn

a_m, b_val = simplified_smo(C, tol, max_passes, X_m, Y)

Number of lagrange multipliers still converging: 7
Number of lagrange multipliers still converging: 6
Number of lagrange multipliers still converging: 3
Number of lagrange multipliers still converging: 6
Number of lagrange multipliers still converging: 8
Number of lagrange multipliers still converging: 4
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 3
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 4
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 3
Number of lagrange multipliers still converging: 2
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 1
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0
Number of lagrange multipliers still converging: 0

Support Vectors

#support vectors information
sv_ind = np.nonzero(a_m) #alpha indices
sv_a_m = a_m[sv_ind] #alphas
sv_X_m = X_m[sv_ind] #vectors
sv_Y = Y[sv_ind] #class

print('Number of Support Vectors:', len(sv_a_m))
print('Support Vectors:\n', sv_X_m)
print('Alphas:\n', sv_a_m)

Number of Support Vectors: 12
Support Vectors:
 [[4.01672464 4.95910969]
 [4.58939644 6.24781842]
 [6.42969753 4.23687801]
 [3.35352254 4.06678074]
 [5.29936958 3.58851751]
 [9.47171399 8.02614293]
 [7.07618927 7.11401766]
 [7.76384263 7.68750358]
 [6.44359498 6.87073672]
 [5.55611474 7.46208598]
 [6.86536742 9.13082197]
 [6.66468045 8.32477016]]
Alphas:
 [0.10383806 0.6        0.6        0.02436853 0.50294886 0.15664808
 0.35682867 0.6        0.03845793 0.40089538 0.16180494 0.11652045]

Plot the Support vectors

#color/hue of support vectors is
sv_hue = 4 #some value other than -1, +1 used for class labels
svecs = [y if ai == 0 else sv_hue for ai, y in zip(a_m, df['Y'].to_list())]
df['SV'] = svecs

#scatter plot of data points
#class column Y is passed in as hue
sns.scatterplot(x=cols[0], y=cols[1], hue='SV', data=df)

<AxesSubplot:xlabel='X1', ylabel='X2'>

png

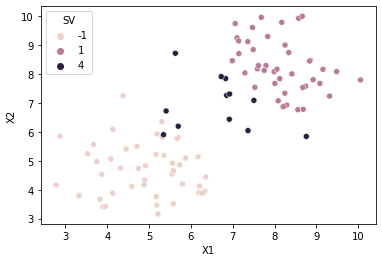
Prediction

Generate Data

Gaussian clusters in 2D numpy arrays

X_m, Y = generate_X_m_and_Y(M, K, n_features, loc_scale) #generate test data points

Predict

Y_pred = [fx(X_m[i], sv_X_m, sv_Y, sv_a_m, b_val) for i in range(M)] #predict (margin of) testing data
Y_pred_class = [-1 if y < 0 else 1 for y in Y_pred] #decision based on predicted margin

Predicted X_m, Y in DataFrame

df = create_df_from_array(X_m, Y, n_features, cols) #create test dataframe
df['Y_pred_margin'] = Y_pred #append the prediction margin column
df['Y_pred_class'] = Y_pred_class #append the class
df.sample(n = 10)

	X1	X2	Y	Y_pred_margin	Y_pred_class
59	7.878629	8.481838	1	2.833952	1
20	5.884862	4.078395	-1	-2.751176	-1
68	9.831908	10.121277	1	5.895153	1
57	7.449198	7.206902	1	1.336733	1
81	6.443595	6.870737	1	0.218461	1
24	4.582161	4.861206	-1	-3.101826	-1
65	7.291804	8.876164	1	2.713573	1
1	5.773598	6.060365	-1	-1.055102	-1
8	3.778248	4.542449	-1	-4.040887	-1
51	8.768240	8.190470	1	3.292608	1

#scatter plot of data points
#class column Y is passed in as hue
sns.scatterplot(x=cols[0], y=cols[1], hue='Y_pred_class', data=df)

<AxesSubplot:xlabel='X1', ylabel='X2'>

png

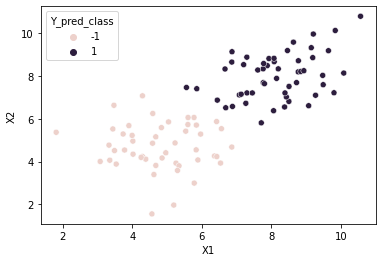
Prediction Accuracy

Y_pred_corr = (Y==Y_pred_class)
num_corr = len(Y_pred_corr[Y_pred_corr == True])
print('Accuracy:', (num_corr/M)*100, '%')

Accuracy: 98.0 %

Converting non-convex primal problem to convex dual problem with affine constraints, and then to convex dual problem with no constraints using Lagrange Multipliers.

Refer CS229 notes while understanding my notes below.

Stanford CS229 Course Notes on SVM
- URL: http://cs229.stanford.edu/summer2020/cs229-notes3.pdf

Functional Margin

10-315 CMU Qatar
- Fall 2019 - Introduction to Machine Learning
- https://web2.qatar.cmu.edu/~gdicaro/10315/lectures/315-F19-14-SVM-1.pdf

The Simplified - Sequential Minimal Optimization (SMO) Algorithm - Support Vector Machines

Stanford CS229 - Andrew Ng

Introduction

Taxonomy

Imports

X_m, Y

Data Configuration

Generate Data

X_m, Y in DataFrame

Model

Model Configuration

Model Prediction Data Structures

Linear Kernel

Predict (eq 2)

Error for a data point (eq 13)

KKT Dual Complementarity Conditions (eq 6-8)

L and H - boundary constraints on alphas (eq 10-11)

n - denominator when calculating optimal alpha_j (eq 14)

alpha_j (eq 12)

clipped / constrained alpha_j (eq 15)

alpha_i (eq 16)

b1, b2, b (eq 17-19)

select random j

Simplified SMO

pseudo-code

python code

Learn

Support Vectors

Plot the Support vectors

Prediction

Generate Data

Predict

Predicted X_m, Y in DataFrame

Prediction Accuracy

Sidebar - Primal to Dual Problem

Converting non-convex primal problem to convex dual problem with affine constraints, and then to convex dual problem with no constraints using Lagrange Multipliers.

Functional Margin

Geometric Margin

Optimization Problem

Lagrangian Duality

Optimal Margin Classifiers

Kernels

Regularization, and SMO