[without library] Iris Flower Species Classification using Multiclass Logistic Regression
[without library] Iris Flower Species Classification using Multiclass Logistic Regression
Based on - Stanford CS231n - Softmax classifier - Andrej Karpathy, and Cross Entropy Loss Derivative - Roei Bahumi
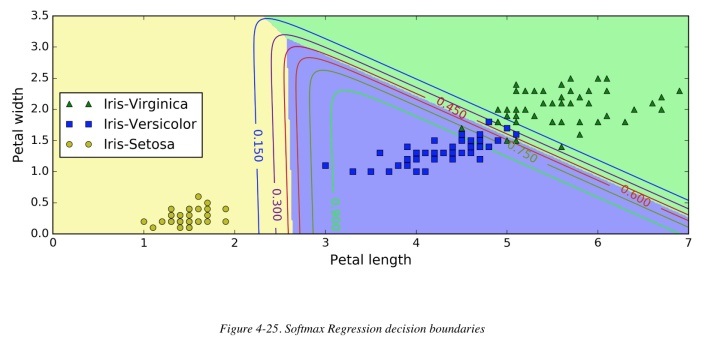
Introduction
This notebook implements Multinomial Logistic Regression. It performs multi-class classification on Iris Flower Species dataset consisting of four attributes and belonging to three classes. There are 300 data points that we divide into training and test data. The prediction accuracy is 94-100%.
Resources:
- Stanford CS231n - Softmax classifier - Andrej Karpathy
- Cross Entropy Loss Derivative - Roei Bahumi
- Generative and Discriminative Classifiers : Naive Bayes and Logistic Regression - Tom Mitchell
- 2020 - Speech and Language Processing - 3rd EDITION - An Introduction to Natural Language Processing - Computational Linguistics and Speech Recognition - Jurafsky - Martin
Towards the end, I have included a sidebar on the Multinomial Logistic Regression.
Taxonomy and Notes
Logistic Regression is a probabilistic classifier. But, it does not model the complete distribution P(X, Y). It is only interested in discriminating among classes. It does that by computing P(Y | X) directly from the training data. Hence, it is a probabilistic-discriminative classifier.
Multinomial Logistic Regression is a composition of K linear functions (K is the number of classes) and the softmax function. Softmax is a generalization of the logistic function to multiple dimensions. It transforms an N-dimensional feature space to a K-dimensional class space. In the case of Iris Flower Species, the N=5 features (bias + sepal/petal length/width) are mapped to K=3 classes. The weight matrix is (N x K), where each column is a linear operator w applied on feature vector x.
It is parametric (weights and bias are the parameters). Binomial Logistic Regression is binary. The model can be modified to use softmax instead of sigmoid, and it becomes Multiclass Logistic Regression.
In summary, Multinomial Logistic Regression is:
- Probabilistic
- Discriminative
- Binary and Multiclass
- Linear
- Parametric
Imports
import numpy as np
import pandas as pd #input
from numpy.random import rand, normal, standard_normal
from numpy import dot, exp
from numpy import mean, std #mean and standard deviation for gaussian probabilities
from scipy.stats import norm #gaussian probabilities
from math import log # to calculate posterior probability
import matplotlib.pyplot as plt
import seaborn as sns
Data
Data Configuration (1 of 2)
Iris Flower Species
f_data = '../input/iris-species/Iris.csv'
f_cols = ['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm', 'Species']
class_colname = 'Species'
Read
read the csv file
#read the csv file
df = pd.read_csv(f_data)
drop unwanted columns
#drop unwanted columns
drop_cols = list(set(df.columns) - set(f_cols))
df = df.drop(drop_cols, axis = 1)
rename last column that supposedly has a class/label
#rename the last column to 'class'
cols = df.columns.to_list()
cols[len(cols)-1] = class_colname
df.columns = cols
sanity check for data getting loaded
df.sample(5)
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | Species | |
|---|---|---|---|---|---|
| 75 | 6.6 | 3.0 | 4.4 | 1.4 | Iris-versicolor |
| 132 | 6.4 | 2.8 | 5.6 | 2.2 | Iris-virginica |
| 89 | 5.5 | 2.5 | 4.0 | 1.3 | Iris-versicolor |
| 35 | 5.0 | 3.2 | 1.2 | 0.2 | Iris-setosa |
| 103 | 6.3 | 2.9 | 5.6 | 1.8 | Iris-virginica |
Data Preprocessing
Helper Functions
visualize
def plot_features_violin(data):
plt.figure(figsize=(15,10))
plt.subplot(2,2,1)
sns.violinplot(data=data, x='Species',y='PetalLengthCm')
plt.subplot(2,2,2)
sns.violinplot(data=data, x='Species',y='PetalWidthCm')
plt.subplot(2,2,3)
sns.violinplot(data=data, x='Species',y='SepalLengthCm')
plt.subplot(2,2,4)
sns.violinplot(data=data, x='Species',y='SepalWidthCm')
normalize
'''normalize the features
return:
copy of the passed in (dataframe), but now with normalized values
parameters:
df: (dataframe) to normalize
cols: (list) of columns to normalize
'''
def normalize(df, cols):
df2 = df.copy(deep = True)
for col in cols:
mu = df2[col].mean()
sigma = df2[col].std()
df2[col] = (df2[col] - mu) / sigma
return df2
Normalize
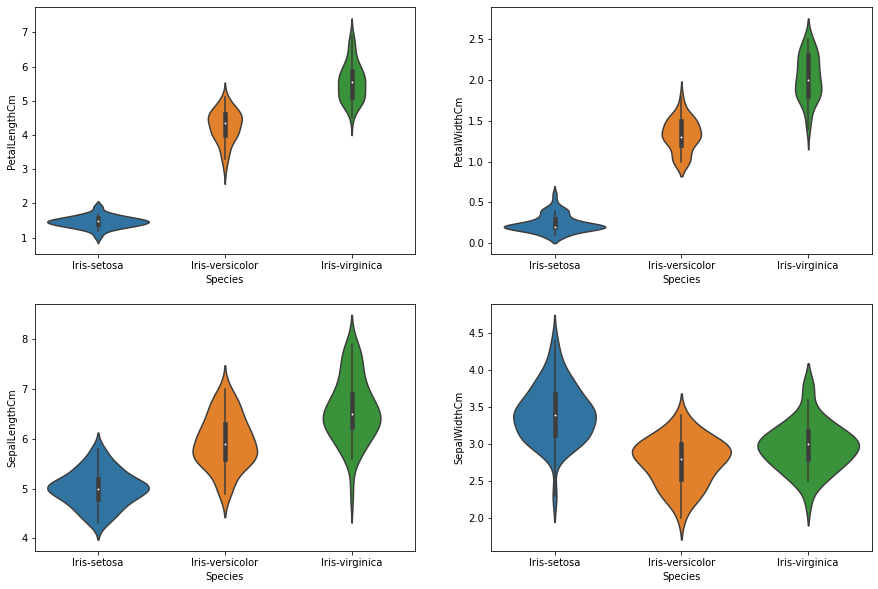
print('Before normalization:\n')
plot_features_violin(df)
Before normalization:
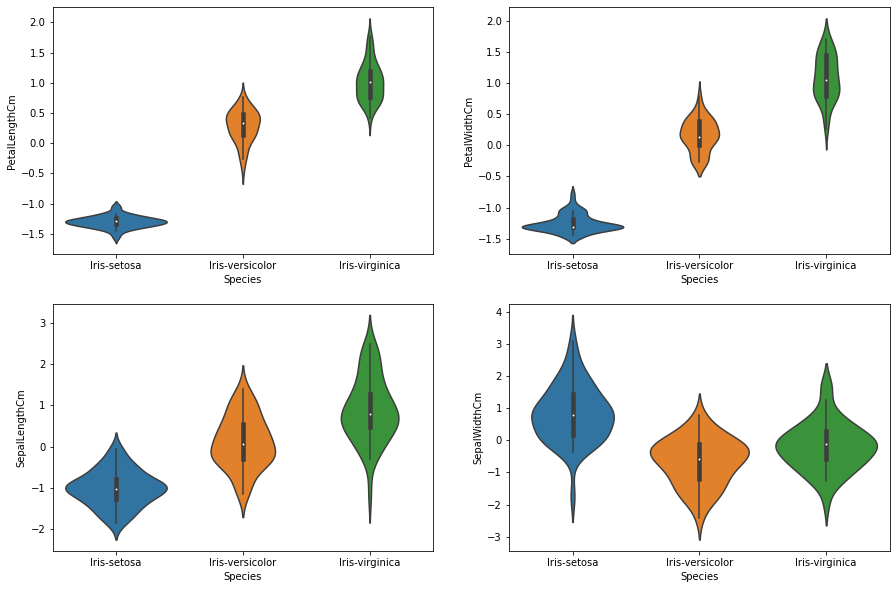
print('\n\nAfter normalization: The relative distribution is still maintained,\
though the range of values is around 0. (see y-axis markers)\n')
df_norm = normalize(df, f_cols[:-1])
plot_features_violin(df_norm)
After normalization: The relative distribution is still maintained, though the range of values is around 0. (see y-axis markers)
Data Configuration (2 of 2)
M: number of data points; N: number of features; K: number of classes
#number of data points, number of attributes
M, N = df_norm.shape[0], df_norm.shape[1]
#number of classes
K = len(df_norm[class_colname].unique())
M, N, K
(150, 5, 3)
Class Names
C = df_norm[class_colname].unique()
C
array(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'], dtype=object)
X_mn, Y
X_mn
The data points matrix X_mn is a M x N matrix, M being the number of data points, N being the number of attributes
#X_mn: first column is the first input '1' for bias
X_mn = np.ones((M, N), dtype=float)
X_mn[:, 1:] = df_norm.loc[:, df_norm.columns != class_colname].to_numpy()
X_mn.shape
(150, 5)
Y
#Y: class column
Y = np.array(M, dtype=float)
#encode class name to offset in C: array of class names
Y = [np.where(C == c_name)[0][0] for c_name in (df_norm.loc[:, df_norm.columns == class_colname].to_numpy())]
Y = np.array(Y, dtype=int)
Y.shape
(150,)
Model
Model Configuration
loc, scale = 0, 0.1 #to initialize weights
train_ds_percent = 0.8 #to split data into train and test
alpha = 0.001 #learning rate
diff_loss = 0.0001### Model Configuration
Model Prediction Data Structures
W
The weight matrix is an N x K matrix, N being the number of attributes, and K being the number of classes
#initliaze weights randomly
W_nk = normal(loc = loc, scale = scale, size = (N, K))
W_nk.shape
(5, 3)
Predict
softmax
The equation above shows the softmax calculated for element ‘i’ of the vector Z. Each Z has K elements (K = no. of classes). The function below performs a vector version of softmax, calculating softmax for each element of vector Z and returning the vector of softmax values.
#softmax: normalize each element of Z and return the normalized vector
def softmax_vec(Z):
# matrix division:
# numerator: exponentiate each element of Z
# denominator: exponentiate each element of Z, and then sum them up
# division: divide each element in the numerator by the sum to normalize it
return exp(Z) / sum([exp(Z_k) for Z_k in Z])
Y_predicted
#predict K probabilities for each data point in 1..M
# and return a M xK matrix of probabilities
def Y_predicted(X_mn, W_nk):
Z_mk = dot(X_mn, W_nk)
#each row Z of Z_mk is passed to softmax to normalize it.
#Y_pred now has a stack of M normalized Z's.
#Each Z has K elements (K = no. of classes)
#so, now, for each data point, we have K probabilities,
# each telling the probability of the data point belonging to class k = 1..K
Y_pred = np.stack([softmax_vec(Z) for Z in Z_mk])
return Y_pred # M x K matrix
Cost (cross-entropy loss)(negative log likelihood loss)
'''Cross-Entropy Loss
returns:
(float) cross-entropy loss from predictions
parameters:
Y_pred: (M.K array) (numDataPoints.numClasses) predicted class probabilities for M data points
Y: (M.1 array) (numDataPoints) actual class for M data points
'''
def Loss_ce(Y_pred, Y):
L_ce = 0.0
for m, k in enumerate(Y):
L_ce += (-1)*log(Y_pred[m][k])
return L_ce
Loss_ce(Y_predicted(X_mn, W_nk), Y)
168.64146013824276
Gradient
def gradients(X_mn, Y, Y_pred, N, K):
#gradient along each of the N attributes, for each of the K classes
grads = np.zeros((N, K), dtype=float)
for j in range(N):
for k in range(K):
for m, X in enumerate(X_mn):
grads[j][k] += (Y_pred[m][k] - (int)(Y[m]==k))*X[j]
return grads
gradients(X_mn, Y, Y_predicted(X_mn, W_nk), N, K)
array([[ -0.39155471, 2.19089601, -1.7993413 ],
[ 46.39999389, 2.24131206, -48.64130594],
[-46.75856991, 31.37213789, 15.38643202],
[ 62.30179774, -6.00141406, -56.30038368],
[ 59.5940192 , -0.19498116, -59.39903804]])
Training Algorithm
def train(X_mn, Y, W_nk):
Y_pred = Y_predicted(X_mn, W_nk) #predicted probabilities
prev_loss = Loss_ce(Y_pred, Y) #loss to begin with
dLdW = gradients(X_mn, Y, Y_pred, N, K) #gradient along each of the N attributes, for each of the K classes
W_nk = W_nk - (alpha * dLdW) #apply learning_rate*gradient to the weights
Y_pred = Y_predicted(X_mn, W_nk) #predicted probabilities with new weights
new_loss = Loss_ce(Y_pred, Y) #predicted probabilities with new weights
#summary print
i_print = 0
#while the loss function is still converging rapidly
while (prev_loss - new_loss > diff_loss):
if(i_print % 500) == 0:
print('Cost:', new_loss)
prev_loss = new_loss #backup the loss to previous loss for convergence detection
dLdW = gradients(X_mn, Y, Y_pred, N, K) #gradient along each of the N attributes, for each of the K classes
W_nk = W_nk - (alpha * dLdW) #apply learning_rate*gradient to the weights
Y_pred = Y_predicted(X_mn, W_nk) #predicted probabilities with new weights
new_loss = Loss_ce(Y_pred, Y) #predicted probabilities with new weights
i_print += 1
return W_nk
Learn
Divide data into Train and Test
mask = rand(M) < train_ds_percent
X_tr, Y_tr, X_te, Y_te = X_mn[mask], Y[mask], X_mn[~mask], Y[~mask]
X_tr.shape, Y_tr.shape, X_te.shape, Y_te.shape
((116, 5), (116,), (34, 5), (34,))
Learn
W_nk = train(X_tr, Y_tr, W_nk)
Cost: 116.6483283544849
Cost: 18.249658848820356
Cost: 12.951954448719748
Cost: 10.645191711359773
Cost: 9.324411602909944
Cost: 8.452276659013673
Cost: 7.824010517344139
Cost: 7.344201154723735
Cost: 6.962156632256088
Cost: 6.648325577035544
Cost: 6.384245774778408
Cost: 6.157746375601451
Cost: 5.960451836587583
Cost: 5.786392123110191
Cost: 5.6311851365748495
Cost: 5.491533384283073
Cost: 5.36490201563757
Cost: 5.249306026851437
Cost: 5.14316558536557
Cost: 5.045205207521434
Cost: 4.954381949702238
Cost: 4.8698332639541295
Cost: 4.790838471178479
Cost: 4.716789847874346
Cost: 4.647170618675076
Cost: 4.581537988365074
Cost: 4.519509904618752
Cost: 4.460754619121964
Cost: 4.404982373239275
Cost: 4.351938714714369
Prediction
Predict
Y_pred_k = [np.argmax(y_pred_k) for y_pred_k in Y_predicted(X_te, W_nk)]
Prediction Accuracy
matches = sum([int(pred==actual) for pred, actual in zip(Y_pred_k, Y_te)])
print('Accuracy is', (matches*100)/len(Y_te), 'percent.')
Accuracy is 94.11764705882354 percent.
Sidebar - Multiclass Logistic Regression
Why Softmax?

Why linear?
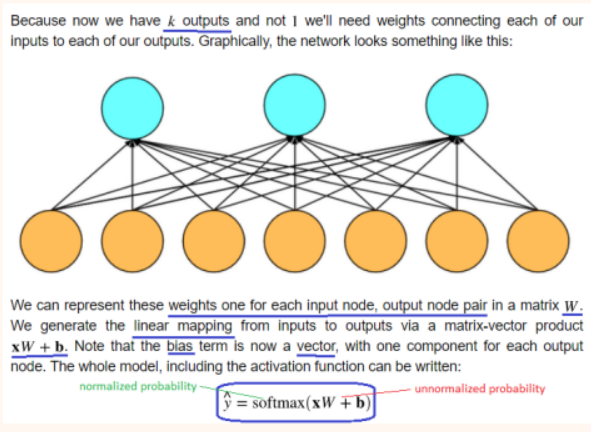
x has unnormalized probabilities, y_cap has normalized probabilities.
Generalization of sigmoid to softmax

Negative Log-Likelihood Loss

Derivation of Eq.5.37 (gradient for a single example)
