SciPy Playground
NumPy provides some functions for Linear Algebra, Fourier Transforms and Random Number Generation, but not with the generality of the equivalent functions in SciPy.
Imports
#multi-dimensional array
import numpy as np
from numpy import vstack #vertical stacking of arrays
#random sampling from distributions
from numpy.random import rand, randn, normal, standard_normal
#data normalization
from scipy.cluster.vq import whiten
#clustering
from scipy.cluster.vq import kmeans #clustering algorithm
#optimization
from scipy import optimize
#classification
#vector quantization - quantizing (labeling) vectors by
# comparing them with centroids
from scipy.cluster.vq import vq
#put ndarrays into a dataframe for plotting
import pandas as pd
#visualizations
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
#sns - Samuel Norman “Sam” Seaborn -
# on the television serial drama The West Wing
import seaborn as sns
#representing sparse martices
from scipy.sparse import csr_matrix # 'compressed sparse row' matrix
from scipy.sparse import dok_matrix # 'dictionary of keys' matrix
#integration
from scipy.integrate import quad, dblquad
#interpolation
from scipy import interpolate
from scipy.interpolate import interp1d
#generated data
import generate_data as gd
scipy.interpolate
https://www.tutorialspoint.com/scipy/scipy_interpolate.htm
plot a function of x
cos ( (x_square/3) + 4)
#a set of equidistant points within an interval
x = np.linspace (0, 4, 12)
#a function of x
#cos ( (x_square/3) + 4)
y = np.cos (((x**2)/3) + 4)
#plot
sns.scatterplot (x, y)
plt.show ()
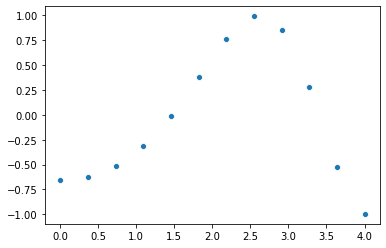
using interpolation, fit a function to the points
f1d_lin = interp1d (x, y, kind = 'linear')
f1d_cub = interp1d (x, y, kind = 'cubic')
x_val = 2
print ('1D Linear interpolation estimate for x =', x_val,\
':', f1d_lin (x_val))
print ('1D Cubic interpolation estimate for x =', x_val,\
':', f1d_cub (x_val))
1D Linear interpolation estimate for x = 2 : 0.5734566736497806
1D Cubic interpolation estimate for x = 2 : 0.5820766474144136
Note
- if we reduce the number of points on which interpolation was performed, we see the effect of cubic interpolation error due to overfitting
- for x = np.linspace (0, 4, 6)
- 1D Linear interpolation estimate for x = 2 : 0.5376240708619846
- 1D Cubic interpolation estimate for x = 2 : 0.6162970299094371
plot the interpolation output
x_vals = np.linspace (0, 4, 30) #input x to the learnt functions
y_vals_lin = f1d_lin (x_vals) #output y from the learnt linear function
y_vals_cub = f1d_cub (x_vals) #output y from the learnt cubic function
plt.plot (x, y, 'o',\
x_vals, y_vals_lin, '-',\
x_vals, y_vals_cub, '--')
plt.show ()
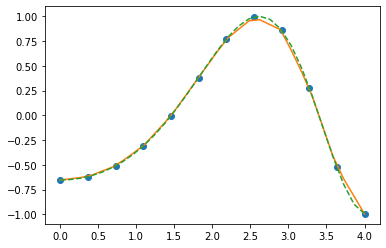
scipy.integrate
http://kitchingroup.cheme.cmu.edu/blog/2013/02/02/Integrating-functions-in-python/
integrands
#x_square
def integrand_single (x):
return x**2
# $x$y y.sin(x) + x.cos(y)
#inner-most integral variable should be the first parameter
def integrand_double (y, x):
return y * np.sin (x) + x * np.cos (y)
evaluate
# integrate x_square
# x = 0..1
ans, err = quad (integrand_single, 0, 1)
print ('\nintegrate x_square from x = 0..1:', ans, err)
# $x$y y.sin(x) + x.cos(y)
# π<=x<=2π
# 0<=y<=π
#We have to provide callable functions for the range of the y-variable.
#Here they are constants, so we create lambda functions
# that return the constants.
ans, err = dblquad (integrand_double, np.pi, 2 * np.pi,\
lambda x: 0, lambda x: np.pi)
print ('\nintegrate $x$y y.sin(x) + x.cos(y) from\n π<=x<=2π and 0<=y<=π:',\
ans, err)
integrate x_square from x = 0..1: 0.33333333333333337 3.700743415417189e-15
integrate $x$y y.sin(x) + x.cos(y) from
π<=x<=2π and 0<=y<=π: -9.869604401089358 1.4359309630105241e-13
scipy.optimize
https://towardsdatascience.com/optimization-with-scipy-and-application-ideas-to-machine-learning-81d39c7938b8
Using SciPy gives you deep insight into the actual working of the algorithm as you have to construct the loss metric yourself and not depend on some ready-made, out-of-the-box function.
Single-Variate Objective Functions
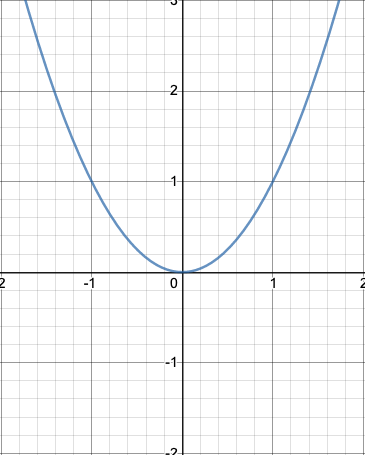
Plot and Definition
#parabola
def parabola (x):
return x**2
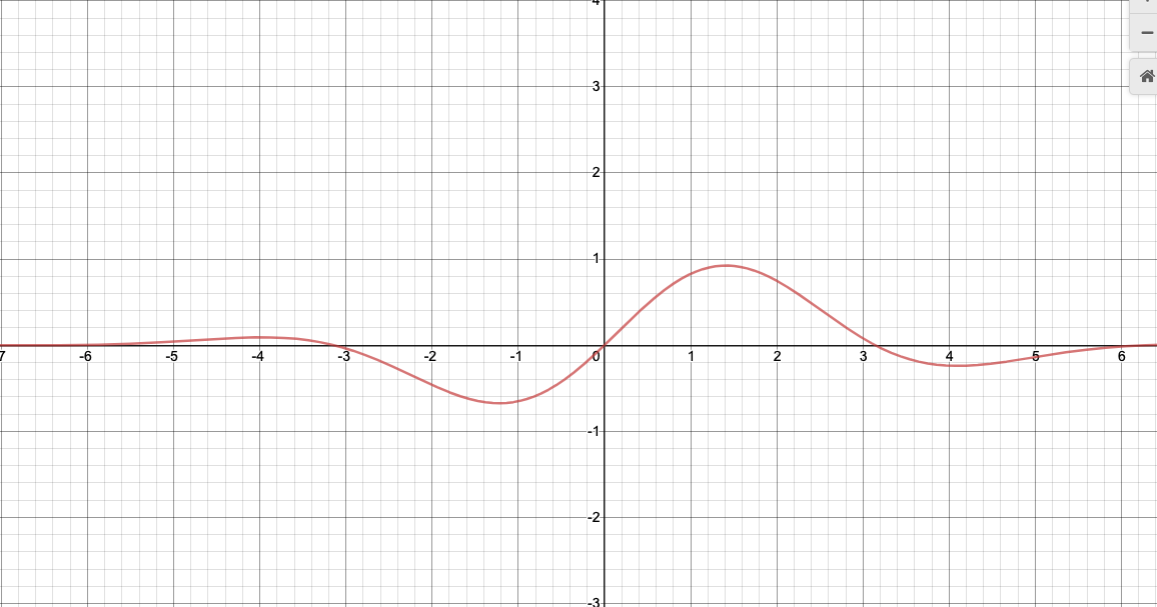
#exotic - sin (x) * exp [-0.1 (x - 0.6)^2]
def sinx_exp (x):
return np.sin (x) * np.exp (-0.1 * ((x - 0.6) ** 2))
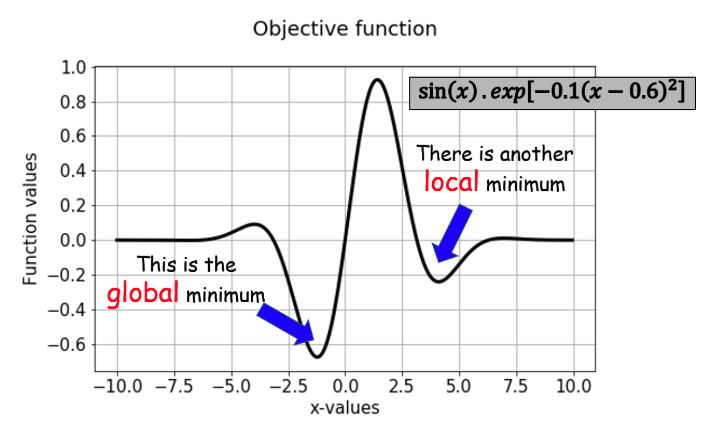
Optimization
1. without constraints, without bounds
optimize.minimize_scalar (objfn)
result = optimize.minimize_scalar (parabola)
print ('minimum of parabola:\n', result)
result = optimize.minimize_scalar (sinx_exp)
print ('\nminimum of sinx_exp:\n', result)
minimum of parabola:
fun: 0.0
nfev: 8
nit: 4
success: True
x: 0.0
minimum of sinx_exp:
fun: -0.6743051024666711
nfev: 15
nit: 10
success: True
x: -1.2214484245210282
2. with bounds (constraints)
- For sinx-exp, mention bounds on x so as to favor local minimum
optimize.minimize_scalar (objfn, bounds = , method = ‘Bounded’)
result = optimize.minimize_scalar (sinx_exp, bounds = (0, 10), \
method = 'Bounded')
print ('\nminimum of sinx_exp:\n', result)
minimum of sinx_exp:
fun: -0.24037563941326692
message: 'Solution found.'
nfev: 12
status: 0
success: True
x: 4.101466164987216
3. with other functional constraints
sinx_exp constraints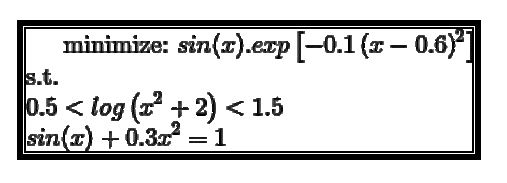
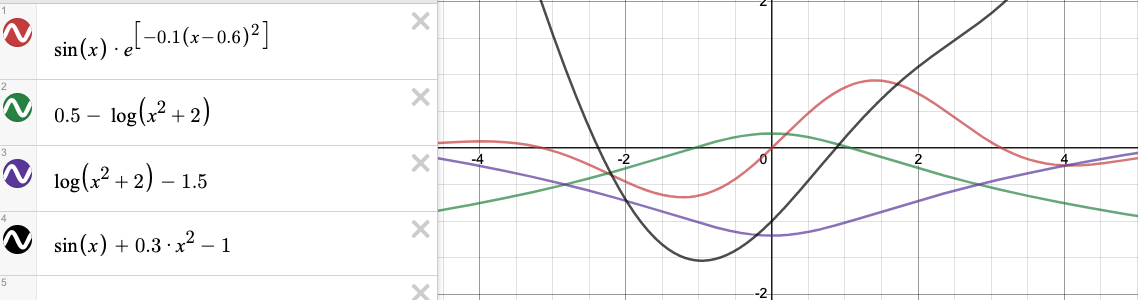
def constraint1 (x):
return (0.5 - np.log10 (x**2 + 2))
def constraint2 (x):
return (np.log10 (x**2 + 2) - 1.5)
def constraint3 (x):
return (np.sin (x) + (0.3 * (x**2)) - 1)
print ('Graphically, constraints met at x = -2.3757.')
print ('Passing x = -2.3757 in constraint functions:\n')
print ('Constraint #1 < 0:', constraint1 (-2.3757))
print ('Constraint #2 < 0:', constraint2 (-2.3757))
print ('Constraint #3 = 0 (almost equal to 0):', constraint3 (-2.3757))
#prepare a dictionary for each constraint
con1 = {'type': 'ineq', 'fun': constraint1} #Inequality
con2 = {'type': 'ineq', 'fun': constraint2} #Inequality
con3 = {'type': 'eq', 'fun': constraint3} #Equality
#prepare a tuple of constraints
cons = (con1, con2, con3)
print (type(con1))
print (type(con2))
print (type(con3))
#print (type(con))
#for ic, con in cons:
#print (ic, con)
Graphically, constraints met at x = -2.3757.
Passing x = -2.3757 in constraint functions:
Constraint #1 < 0: -0.38331786545918767
Constraint #2 < 0: -0.6166821345408123
Constraint #3 = 0 (almost equal to 0): 4.4798883980234905e-06
<class 'dict'>
<class 'dict'>
<class 'dict'>
optimize.minimize (objfn, bounds = , method = ‘Bounded’)
SciPy allows handling arbitrary constraints through the more generalized method optimize.minimize.
Note:
- not all methods in the minimize function support constraint and bounds).
- Here we chose SLSQP method which stands for sequential least-square quadratic programming
- to use minimize we need to pass on an initial guess in the form of x0 argument
This code fails to optimize
result = optimize.minimize (sinx_exp, x0 = 0, method = 'SLSQP', \
constraints = cons,\
options = {'maxiter': 100})
print ('\nminimum of sinx_exp:\n', result)
print ('\nNote the ERROR!!!: success: False')
minimum of sinx_exp:
fun: array([0.76316959])
jac: array([0.59193639])
message: 'Iteration limit reached'
nfev: 392
nit: 100
njev: 100
status: 9
success: False
x: array([0.8773752])
Note the ERROR!!!: success: False
provide a suitable initial guess of x0 = -2
result = optimize.minimize (sinx_exp, x0 = -2, method = 'SLSQP', \
constraints = cons,\
options = {'maxiter': 100})
print ('\nminimum of sinx_exp:\n', result)
print ('\nNote the SUCCESS!!!: success: True')
minimum of sinx_exp:
fun: array([-0.28594945])
jac: array([-0.46750661])
message: 'Positive directional derivative for linesearch'
nfev: 12
nit: 76
njev: 6
status: 8
success: False
x: array([-2.37569791])
Note the SUCCESS!!!: success: True
reduce the number of iterations from 100 down to 3
This code fails with iteration limit, but succeeds to get good enough optimization
result = optimize.minimize (sinx_exp, x0 = -2, method = 'SLSQP', \
constraints = cons,\
options = {'maxiter': 3})
print ('\nminimum of sinx_exp:\n', result)
print ('\nNote the FAILURE!!!: success: False')
print ('But, the resultant x is close to the success case.')
minimum of sinx_exp:
fun: array([-0.2854205])
jac: array([-0.46737936])
message: 'Iteration limit reached'
nfev: 6
nit: 3
njev: 3
status: 9
success: False
x: array([-2.37682949])
Note the FAILURE!!!: success: False
But, the resultant x is close to the success case.
Multi-variate Objective Functions
Plot and Definition
Gaussian Mixture
- gauss 1: mean = -1, sd = 2.1
- gauss 2: mean = 0.3, sd = 0.8
- gauss 1: mean = 2.1, sd = 1.7
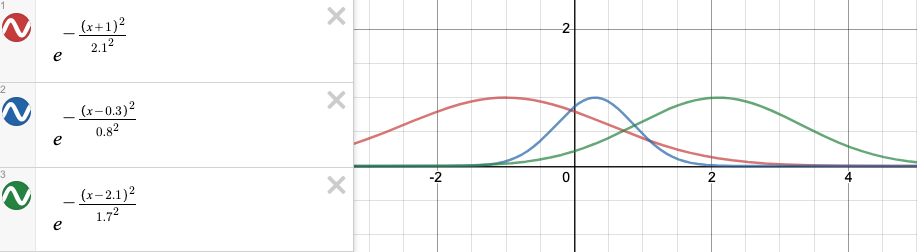

#expects a vetor x
def gaussian_mixture (x):
gausses = []
for i in range (len(x)):
gauss = np.exp (-((x[i]-means[i])**2)/(stds[i]**2))
gausses.append (gauss)
#objective function is formulated as a function to be minimized
#maximizing the gaussians is minimizing their negative
return -1 * sum(gausses)
Optimization
Unbounded Inputs - optimize.minimize (objfn, method = ‘SLSQP’)
- gauss 1: mean = -1, sd = 2.1
- gauss 2: mean = 0.3, sd = 0.8
- gauss 1: mean = 2.1, sd = 1.7
Note:
- we get back a vector instead of a scalar
- the code below returns an array of means of the respective distributuions.
means = [-1, 0.3, 2.1]
stds = [2.1, 0.8, 1.7]
initial_guess = np.zeros ((3))
result = optimize.minimize (gaussian_mixture, x0 = initial_guess,\
method = 'SLSQP',\
options = {'maxiter': 100})
print (result)
print ('\nObserve that x is the means of the respective distributuions')
fun: -2.9999996182234456
jac: array([-8.10027122e-05, -2.40176916e-04, 7.11083412e-04])
message: 'Optimization terminated successfully'
nfev: 34
nit: 8
njev: 8
status: 0
success: True
x: array([-1.00017856, 0.29992314, 2.1010275 ])
Observe that x is the means of the respective distributuions
Bounded Inputs - optimize.minimize (objfn, bounds = , method = ‘SLSQP’)
If the sub-process settings can occupy only a certain range of values (some must be positive, some must be negative, etc.) then the solution will be slightly different — it may not be the global optimum.
means = [-1, 0.3, 2.1]
stds = [2.1, 0.8, 1.7]
initial_guess = np.zeros ((3))
x1_bound = (-2,2)
x2_bound = (0,5)
x3_bound = (-3,0)
bounds = (x1_bound, x2_bound, x3_bound)
result = optimize.minimize (gaussian_mixture, x0 = initial_guess,\
method = 'SLSQP',\
options = {'maxiter': 100},\
bounds = bounds)
print (result)
print ('\nObserve that x1 and x2 are still the means, \
while x3 has reduced to almost 0 due to the constraint.')
fun: -2.2174140557543054
jac: array([-2.89082527e-06, 3.59982252e-04, -3.15965086e-01])
message: 'Optimization terminated successfully'
nfev: 25
nit: 6
njev: 6
status: 0
success: True
x: array([-1.00000636, 0.30011519, 0. ])
Observe that x1 and x2 are still the means, while x3 has reduced to almost 0 due to the constraint.
scipy.cluster
cluster settings
num_points = 100
num_dim = 2
num_clusters = 5
cluster_distance = 1
normalize = True
plot the data
#generate cluster data
df = gd.generate_cluster_data (num_points, \
num_dim, num_clusters, cluster_distance, \
normalize)
#plot the prepared data and its normalized form
fig, ax = plt.subplots (1, 2)#, figsize = (8, 8))
#parameters are created from column names using *[list]
sns.scatterplot (*(list(df.columns [:num_dim])), 'label_train',\
data = df, ax = ax [0])
#from col# num_dim to col# 2*num_dim, say, from col 2 to col 4 (excluding)
sns.scatterplot (*(list(df.columns [num_dim:2*num_dim])), 'label_train',\
data = df, ax = ax [1])
plt.show ()

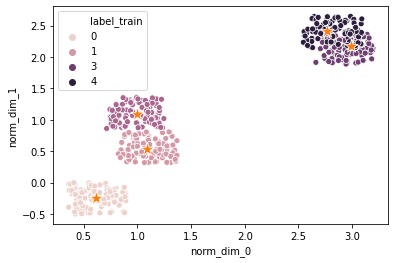
cluster the data
centroids = kmeans (data, n_clusters)
labels = vq (data, centroids)
# algorithm
data_norm = df [df.columns [num_dim:-1]].to_numpy ()
centroids, _ = kmeans (data_norm, num_clusters)
# classification
label_test, _ = vq (data_norm, centroids)
# plot
#plot the points
sns.scatterplot (*(list(df.columns [num_dim:2*num_dim])), 'label_train',\
data = df)
#plot the centroids
sns.scatterplot (centroids [:, 0], centroids [:, 1],\
marker = '*', s = 200)
plt.show ()
scipy.sparse, Sparse Matrix
Data Structures
Data
mat = np.array ([[1, 0, 0, 1, 0, 0], [0, 0, 2, 0, 0, 1],\
[0, 0, 0, 2, 0, 0]])
print ('2D array:\n', mat)
2D array:
[[1 0 0 1 0 0]
[0 0 2 0 0 1]
[0 0 0 2 0 0]]
CSR (compressed sparse row) form
mat_csr = csr_matrix (mat)
print ('Compressed Sparse Row (CSR) form of 2D array:\n', mat_csr)
print ('CSR internals:\n', 'data: ', mat_csr.data,\
'index pointer: ', mat_csr.indptr, 'indices: ', mat_csr.indices)
mat_dense_from_csr = mat_csr.todense ()
print ('Dense array got back from CSR form:\n', mat_dense_from_csr)
Compressed Sparse Row (CSR) form of 2D array:
(0, 0) 1
(0, 3) 1
(1, 2) 2
(1, 5) 1
(2, 3) 2
CSR internals:
data: [1 1 2 1 2] index pointer: [0 2 4 5] indices: [0 3 2 5 3]
Dense array got back from CSR form:
[[1 0 0 1 0 0]
[0 0 2 0 0 1]
[0 0 0 2 0 0]]
NOTE on CSR internals:
- indices [0, 3] are for row_0, [2, 5] are for row_1, [3] is for row_2
- indptr 0 points to start of row_0 indices, and 2 points to start of row_1 indices, etc
DoK (dictionary of keys) form
mat_dok = dok_matrix (mat)
print ('Dictionary of Keys (DoK) form of 2D array:\n',\
list (mat_dok.items()))
mat_dense_from_dok = mat_dok.todense ()
print ('Dense array got back from DoK form:\n', mat_dense_from_dok)
Dictionary of Keys (DoK) form of 2D array:
[((0, 0), 1), ((0, 3), 1), ((1, 2), 2), ((1, 5), 1), ((2, 3), 2)]
Dense array got back from DoK form:
[[1 0 0 1 0 0]
[0 0 2 0 0 1]
[0 0 0 2 0 0]]
Calculate Sparsity
np.count_nonzero(ndarray) and np.ndarray.size
print ('Non-Zero count: ', np.count_nonzero (mat))
print ('Size: ', mat.size)
Non-Zero count: 5
Size: 18
density = nonzero_count / size sparcity = 1 - density
print ('Sparsity: ', 1 - (np.count_nonzero (mat) / mat.size))
Sparsity: 0.7222222222222222